Description

Permutation Sequence

The set [1,2,3,...,n] contains a total of n! unique permutations.

By listing and labeling all of the permutations in order, we get the following sequence for n = 3:

  1. "123"
  2. "132"
  3. "213"
  4. "231"
  5. "312"
  6. "321"

Given n and k, return the k-th permutation sequence.

Note:

  • Given n will be between 1 and 9 inclusive.
  • Given k will be between 1 and n! inclusive.

Example 1:

Input: n = 3, k = 3
Output: "213"

Example 2:

Input: n = 4, k = 9
Output: "2314"

假设存在长度为n的数组：[1,2,3,...,n]，输出第k个排列。

Solution

字典序树

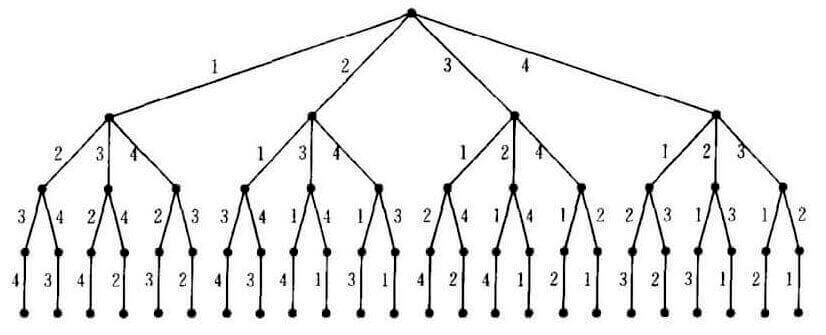
一个长度为n的数组，总共有n!种排列。假设第一个数字固定后，剩余(n-1)!种排列。

上图中的字典序树可以更直观的看出， 在n=4:[1,2,3,4]中， “第零层”包含4!=24个叶子， 第一层包含3!=6个叶子， 第二层包含2!=2个叶子…

假设现在要查找第k=9个排列（第九个叶子），第一层应该经过第⌈9/3!⌉ 个分支，即ceil(k/(n-1)!)。

由此公式，可以依次求每层分支序号。 比如k=9，依次经过：

  1. ⌈9 / 3!⌉: 2
  2. ⌈9-3!*(2-1) / 2!⌉: 2
  3. [9-3!*(2-1)-2!*(2-1) / 1!]: 1
  4. 1

通过序号：2,2,1,1所经过的分支，可以得到结果：2314

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

func getPermutation(n int, k int) string {
    s := []rune{}

    total := 1

    for i := 1; i <= n; i++ {
        total *= i
        s = append(s, rune(i)+rune('0'))
    }

    ret := make([]rune, n)
    idx := 0
    for n > 0 {
        // (n-1)!
        total /= n

        // 当前层索引
        i := (k - 1) / total

        // 移除 s[i]
        ret[idx] = s[i]
        s = append(s[:i], s[i+1:]...)

        // 减去前面组的数量，得到下一层的索引
        k -= total * i
        idx++
        n--
    }

    return string(ret)
}

Similar Problem