Description
Largest Rectangle in Histogram
Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.
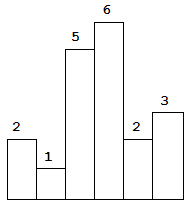
Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].
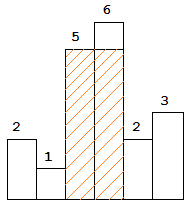
The largest rectangle is shown in the shaded area, which has area = 10 unit.
给出一个直方图,求最大矩形面积。
Solution
首先假设直方图是升序的,比如:1, 3, 5, 6, 7
那么需要比较的面积有:1*5,3 * 4,5*3,6*2,7*1。
计算公式为:$ S(i) = height[i] * (length-i) $
所以最大面积:$ \max_{i=0}^n{S(i)} $
那遇到无序的数组怎么办呢?
根据提示可以是用栈,目的是用于构造升序数组:
假设当前高度为h:
- 如果升序则直接入栈
- 遇到降序,将栈中所有比
h高的都利用公式计算出面积,然后降低它们的高度至h,使数组重新有序
例如数组1, 3, 4, 2, 3:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| ^
| 0
| 00 0
| 0000
| 00000
.------->
首先:1,3,4 都是升序,依次入栈(下标入栈):
^
| 0 stack:
| 00 [2]
| 00 [1]
| 000 [0]
.------->
遇到:2,不符合升序,计算前面 3 和 4 的面积分别为:S(1)=3*2,S(2)=4*1
然后降低高度至 2
^
| stack: 将 4 的下标出栈,保留 3 的下标(因为 3 所在位置是新高度的起点)
|
| 000 [1]
| 0000 [0]
.------->
遇到:3,符合升序,直接入栈
^
| stack:
| 0 [4]
| 0000 [1]
| 00000 [0]
.------->
最后仍需要计算的面积有:S(0)=1*5,S(1)=2*4,S(4)=3*1
所以最大面积为 8
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
| func maxInt(a, b int) int {
if a > b {
return a
}
return b
}
func largestRectangleArea(heights []int) int {
stack := make([]int, 0)
lenStack := len(stack)
max := 0
// 追加一个 -1,用于最后清空栈
heights = append(heights, -1)
for i := 0; i < len(heights); i++ {
h := heights[i]
if lenStack > 0 && h < heights[stack[lenStack-1]] {
// 如果前面更高,将更高的都出栈
// 同时计算面积,然后降低它们的高度(形成新的“有序”)
for {
idx := stack[lenStack-1]
// 计算面积
max = maxInt(max, heights[idx]*(i-idx))
// 降低高度
heights[idx] = h
lenStack-- // 假出栈
if lenStack == 0 || h > heights[stack[lenStack-1]] {
// 最后一个,保留在栈中作为新高度的起点
lenStack++
break
}
stack = stack[:lenStack]
}
} else /* 这个判断可有可无 if lenStack == 0 || h > heights[stack[lenStack-1]] */ {
// 将当前索引入栈
stack = append(stack, i)
lenStack++
}
}
return max
}
|
Similar Problem

